Magnetic Resonance Elastography

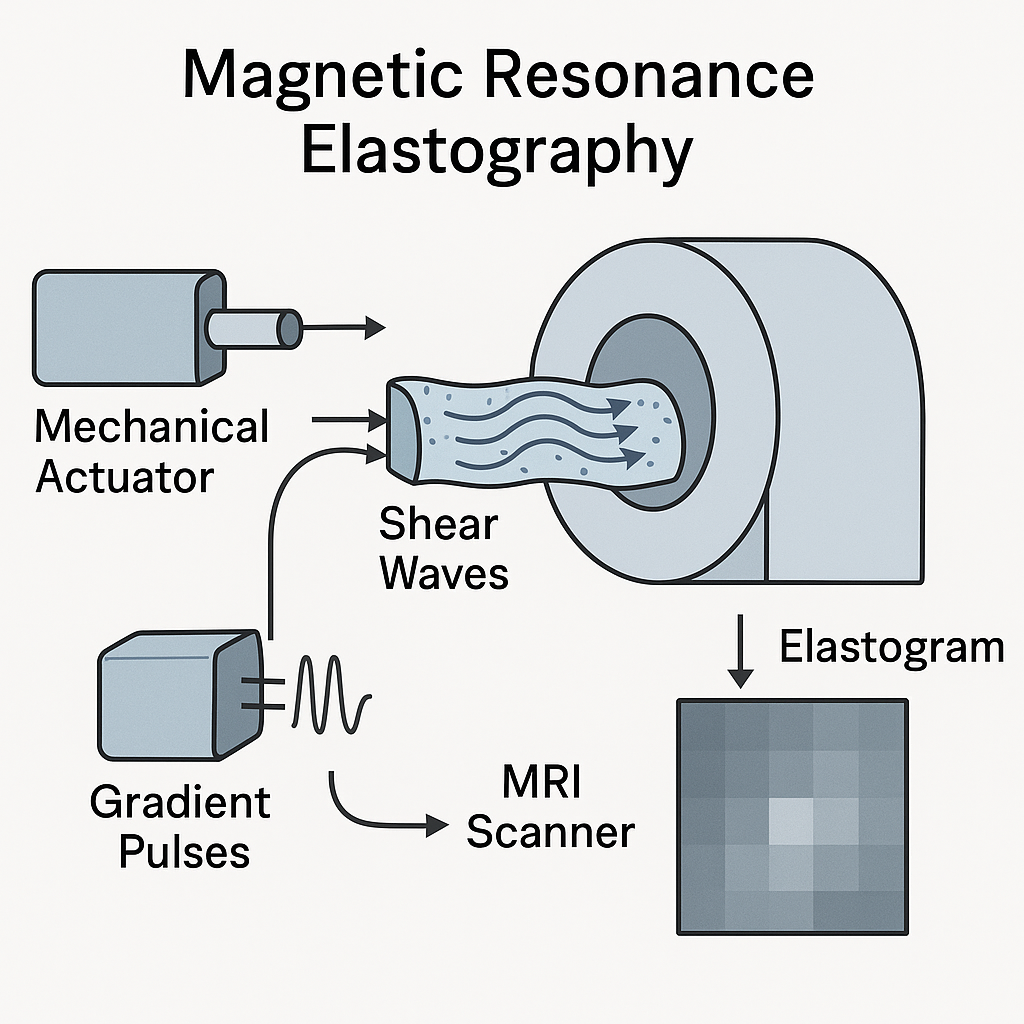Magnetic Resonance Elastography (MRE) is a non-invasive imaging technique that combines magnetic resonance imaging with externally induced shear waves to quantitatively map tissue mechanical properties. A mechanical actuator vibrates at low frequencies (typically $20$–$200\ \mathrm{Hz}$, $10^1$–$10^2\ \mathrm{Hz}$), generating shear waves with wavelengths $\lambda = c_s / f$ on the order of $5$–$50\ \mathrm{mm}$ ($5\times10^{-3}$–$5\times10^{-2}\ \mathrm{m}$), given typical shear wave speeds $c_s \approx 1$–$5\ \mathrm{m/s}$. Wave amplitudes in soft tissue are on the order of $1$–$100\ \mu\mathrm{m}$ ($10^{-6}$–$10^{-4}\ \mathrm{m}$). These dynamic displacements are encoded into the phase of the MRI signal using oscillating motion-encoding gradients ($G \approx 10$–$30\ \mathrm{mT/m}$), producing a phase shift

$$\phi = \gamma \int G(t)\cdot u(t)\,dt$$

where $\gamma$ is the proton gyromagnetic ratio and $u(t)$ the local displacement.

Under harmonic excitation at angular frequency $\omega$, the displacement field $u(\mathbf{r},t)$ satisfies the Helmholtz equation:

$$\nabla^2 u + k^2 u = 0,$$

with wave number $k = \omega / c_s$ and shear wave speed $c_s = \sqrt{\mu/\rho}$. From measured wavelengths ($\lambda = 2\pi/k$) and tissue density $\rho \approx 1000\ \mathrm{kg/m^3}$, one can estimate the shear modulus $\mu = \rho c_s^2$ in the kPa range ($10^3$–$10^4\ \mathrm{Pa}$). For example, $c_s = 2\ \mathrm{m/s}$ yields $\mu \approx 4\ \mathrm{kPa}$.

After acquisition of phase images at multiple vibration phase offsets, inverse mechanical modeling or direct inversion algorithms reconstruct spatial maps of shear modulus—elastograms—with voxel sizes of $\sim1$–$3\ \mathrm{mm}$ and stiffness sensitivity on the order of $1\ \mathrm{Pa}$. MRE is sensitive to stiffness-change associated with pathologies such as liver fibrosis ($\mu$ increases from $\sim2\ \mathrm{kPa}$ in healthy tissue to $\sim5\ \mathrm{kPa}$ in fibrotic tissue) and brain tumors or neurodegenerative disorders.